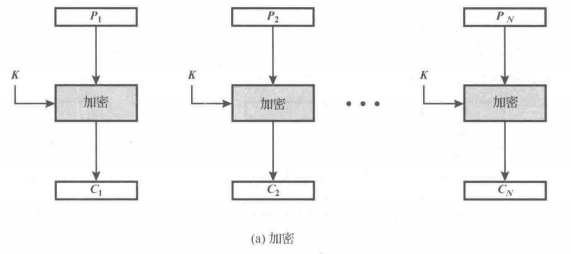
MT19937预测随机数
一、基本介绍
mt19937 ,又称梅森旋转算法,是一个伪随机数生成算法,由松本与西村设计于 1998 年提出,可以快速产生高质量的伪随机数。19937这个名字来源于周期长度为梅森素数 。
Python的“random”标准库使用mt19937,因此我们可以很容易地破解它,以此来预测要生成的随机数。
二、算法
MT19937主要分为三部分:
1.生成一个seed,通过seed初始化624个32位的状态向量
2.根据状态向量生成随机数(这里说的随机数都是32位的)
3.每生成624个随机数,状态向量旋转
所以,只要知道至少连续的624个32位随机数,就能预测此状态之前和之后的随机数。
若随机数不是32位,可以分成32位的整数倍,按照先生成低32位,再生成高位的原则。
三、函数
1.mersenne-twister-recover[]eboda/mersenne-twister-recover: Given at least 624 outputs of a Mersenne Twister PNRG we can restore its internal state. (github.c ...
Groebner基与多元多次方程组的解
一、需求
1.解多元多次方程组
2.环上多项式方程的离散对数问题
二、基本定义
1.理想:
给定环R,I是R的子环,如果对任意的r∈R有rI⊂I和Ir⊂I,则称I是R的理想。给定环R,I是R的子环,\\如果对任意的r\in R有rI\sub I和Ir\sub I,\\则称I是R的理想。
给定环R,I是R的子环,如果对任意的r∈R有rI⊂I和Ir⊂I,则称I是R的理想。
三、过程
对于一个复杂的多元多次多项式G0,无论是求其方程解还是求公因式(欧几里得算法),都很复杂。
我们希望找到一个简单的多项式G,它能保持G0一样的效果。
这就是G0的Groebner basis。
Groebner basis,即G是包含G0的最小理想的生成集。
我的理解是,G0的最小理想是I,G的最小理想也是I。
理想I作为一个中间桥梁,用来生成G。
本人能力有限,看书不求甚解,原理暂不考虑。
所以,求多项式G0等于0的解,就是求Groebner基等于0的解。
四、算法
N=...PR.<x1, x2, x3> = PolynomialRing(Zmod(N))polys = [...]#使用x1,x ...
密码学基础
有限域GF(p)
p为mod p,p须为素数,不然域中无乘法逆元。
有限域GF(p^n),n为正整数,p为素数
n=1,GF§,
n=2,GF(p^2):系数为0或1的多项式,最高次不超过n-1,可以表示成长度为2的矢量
多项式运算
1.Zp中,系数模p运送,p一般为2
2.GF(2^n),系数模2,最高次小于n,对n次多项式取模,加减乘除模实际上是对比特串进行操作
3.Grobner基
p.<a,b>=PolynomialRing(Zmod(p))a、b为多项式生成元
可以用a、b构建多项式,在此多项式环上
椭圆曲线
y2=x3+ax+by^2=x^3+ax+b
y2=x3+ax+b
群定义:
1.群元素:所有群上点
2.单位元:0
3.逆元:关于x轴对称点
4.加法封闭性:一条直线与曲线交的三个点,P+Q+R=0,P+Q=-R,显然-R也在曲线上
5.结合律:显然√
6.交换律:显然√
sage:
Curve=EllipticCurve(F,[a,b])
F代表有限域
Curve.random_point()曲线上随机一点,返回(x,y,z)
Curve.lift_x( ...
CINTA第十一章
为的生成元,且是使之成立的最小值是奇素数,根据欧拉准则若是模的二次剩余,则,与是最小值矛盾,是模的二次非剩余

定义从到的映射满足群同态很明显,中的单位元是为使得的集合定义从在到的映射明显满足同态,且是满同态很明显,中的单位元是为使得明显的单位元为,使得且根据满射,使得根据费马小定理,即有根据费马小定理是成立的使得即根据第一同构定理与同构与同构与同构
CINTA第十章
1.令M=∏i=14mi=3465根据egcda1=1,b1=M/m1=693,b1−1=2 mod 5a2=2,b2=M/m2=495,b2−1=3 mod 7a3=3,b3=M/m3=385,b3−1=4 mod 9a4=4,b4=M/m4=315,b4−1=8 mod 11x=∑i=1n=aibibi−1=19056≡1731 mod M∴x=17311.令M=\prod_{i=1}^4m_i=3465\\
根据egcd\\
a_1=1,b_1=M/m_1=693,b_1^{-1}=2\bmod 5\\
a_2=2,b_2=M/m_2=495,b_2^{-1}=3\bmod 7\\
a_3=3,b_3=M/m_3=385,b_3^{-1}=4\bmod 9\\
a_4=4,b_4=M/m_4=315,b_4^{-1}=8\bmod 11\\
x=\sum_{i=1}^{n}=a_ib_ib_i^{-1}=19056\equiv1731\bmod M\\
\therefore x=1731
1.令M=i=1∏4mi=3465根据egcda1=1,b1=M/m1=69 ...
CINTA第九章
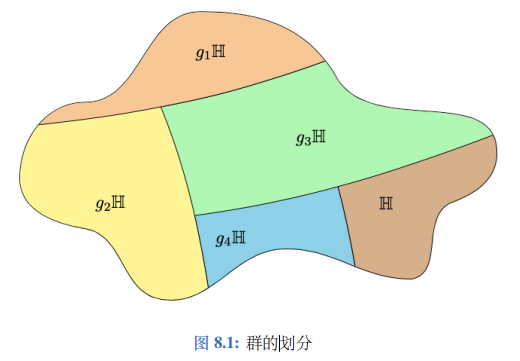
根据命题9.5,H是G的正规子群当且仅当对任意g∈G,有 gHg −1 = H。实 际上,条件可以放松到只证明 gHg −1 ⊂ H。请给出证明。
∵∀g∈G,gHg−1⊂H,∴gH⊂Hg,∴H⊂g−1Hg∴H⊂g−1H(g−1)−1即H⊂gHg−1∵gHg−1⊂H∴gHg−1=H∴gH=Hg∴H是G的正规子群.\because\forall g\in G,gHg^{-1}\subset H,\\
\therefore gH\subset Hg,\\
\therefore H\subset g^{-1}Hg\\
\therefore H\subset g^{-1}H(g^{-1})^{-1}\\
即H\subset gHg^{-1}\\
\because gHg^{-1}\subset H\\
\therefore gHg^{-1}=H\\
\therefore gH=Hg\\
\therefore H是G的正规子群.
∵∀g∈G,gHg−1⊂H,∴gH⊂Hg,∴H⊂g−1Hg∴H⊂g−1H(g−1)−1即H⊂gHg−1∵gHg−1⊂H∴gHg−1=H∴gH=Hg∴H是G的正规子群 ...
CINTA作业四
1.证明命题9.1
1.∵G→H是同构映射,所以G和H是同构的,∵ϕ−1也是双射,且G和H是同构的∴ϕ−1:H→G也是同构.2.∵G→H是双射,显然满足一一对应∴∣G∣=∣H∣3.∵同构,∴任取a,b∈G,有ϕ(a⋅b)=ϕ(a)∘ϕ(b)∵G是阿贝尔群,∴ϕ(a⋅b)=ϕ(b⋅a)=ϕ(b)∘ϕ(a)∴ϕ(a)∘ϕ(b)=ϕ(b)∘ϕ(a)∴H也是阿贝尔群.4.∵G是循环群,∴存在g是G的生成元∵G→G是同构,∴ϕ(g2)=ϕ(g⋅g)=ϕ(g)∘ϕ(g)=ϕ(g)2ϕ(gn)同理,∴∃ϕ(g)为H的生成元,∴H也是循环群5.∵这是一种双射,一一对应∴G的子集G′对应于H的子集H′,阶都是n封闭性:设ϕ(a),ϕ(b)∈H,∴a,b∈G,ab∈G∵ϕ(a⋅b)=ϕ(a)∘ϕ(b)∴ϕ(a)∘ϕ(b)∈G封闭性得证结合律:显然满足单位元:∵a,e∈G,∴ϕ(a),ϕ(e)∈H,ϕ(e⋅a)=ϕ(a)=ϕ(a)∘ϕ(e)即ϕ(e)是单位元逆元:∵a,a−1∈G,∴ϕ(a),ϕ(a−1)∈Hϕ(a⋅a−1)=ϕ(e)=ϕ(a)∘ϕ(a−1)即存在逆元.1.\because G\right ...
CINTA作业四
第六章 群与子群
因为根据结合律g0g1...gn∗gn−1...g1−1g0−1=g0g1...e...g1−1g0−1=e又因为gn−1...g1−1g0−1∗g0g1...gn=g1−1g0−1...e...g0g1...e=e所以g0g1...gn的逆元是gn−1...g1−1g0−1。因为根据结合律g_0g_1...g_n*g_n^{-1}...g_1^{-1}g_0^{-1}\\
=g_0g_1...e...g_1^{-1}g_0^{-1}=e\\
又因为g_n^{-1}...g_1^{-1}g_0^{-1}*g_0g_1...g_n\\
=g_1^{-1}g_0^{-1}...e...g_0g_1...e=e\\
所以g_0g_1...g_n的逆元是g_n^{-1}...g_1^{-1}g_0^{-1}。
因为根据结合律g0g1...gn∗gn−1...g1−1g0−1=g0g1...e...g1−1g0−1=e又因为gn−1...g1−1g0−1∗g0g1...gn=g1−1g0−1...e...g0g1...e=e所以g0g ...
CINTA第三章
1.设p=23和a=3,使用费尔马小定理计算a^2019 mod p
32019≡322∗91+17≡317 mod 2332≡9 mod 2334≡9∗9≡15 mod 2338≡15∗15≡5 mod 23316≡5∗5≡3 mod 23317≡9 mod 23所以32019 mod 23=93^{2019}\equiv3^{22*91+17}\equiv3^{17}\bmod23\\
3^{2}\equiv9\bmod 23\\
3^{4}\equiv9*9\equiv15\bmod 23\\
3^{8}\equiv15*15\equiv5\bmod23\\
3^{16}\equiv5*5\equiv3\bmod23\\
3^{17}\equiv9\bmod 23\\
所以3^{2019}\bmod23=9
32019≡322∗91+17≡317mod2332≡9mod2334≡9∗9≡15mod2338≡15∗15≡5mod23316≡5∗5≡3mod23317≡9mod23所以32019mod23=9
2.使用费尔马小定理求解同余方程x^50=2(mod 17).
x50≡x ...
CINTA第二章
7.手动计算以下模m下a的乘法逆元。(a)m=11,a=5;(b)m=121,a=13;©m=1021,a=131.
8.编写C语言程序完成模指数运算,即给定整数x,y和m为输入,计算并返回x^y mod m
int mod(int x,int y,int m){ int res=1; while(y>0) { if(y&1) res=(res*x)%m; y>>=1; x=(x*x)%m; } return res;}
9.用快速指数运算计算斐波那契数列。
struct mat{ int m[2][2];};mat mult(mat m1,mat m2){ mat temp; memset(temp.m,0,sizeof(temp.m)); for(int i=0;i<2;i++) { for(int j=0;j<2;j++) { for(int k=0;k<2;k++) { temp.m[i][j]=(temp.m[i][j]+m1.m[i][k]*m2.m[k][j])%10000; } } } ret ...