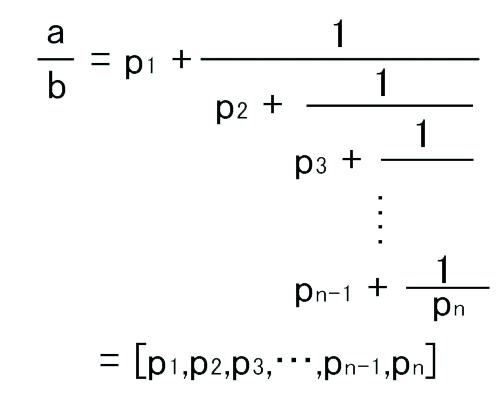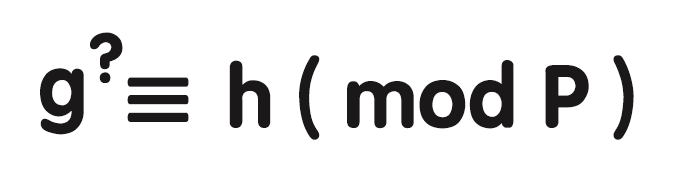关于循环群的一些问题
一、定义
这里引用《CINTA》里的定义。
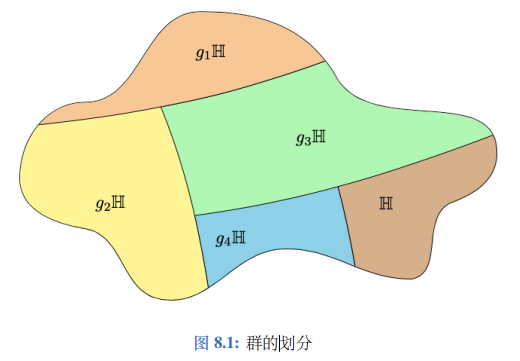
说白了,就是给定一个g,整个群都可以由g生成。但群不一定是有限的。想象一下Z\ZZ就是这种情况,而就是这种情况,而就是这种情况,而\Q和R\RR则找不到生成元。
有限阶的循环群就更特殊了,一般是模一个数。
二、栗子
哪些是循环群?如何判断是否是循环群。
1.找到生成元
2.同构于一个循环群
3.循环群的子群也是循环群(性质)
Z\ZZ是循环群,nZn\ZnZ是循环群。
ZnZ_nZn是循环群。
并且以上默认都为加法群。
Zp∗Z_p^*Zp∗是循环群,举个栗子
Z7∗\Z_7^*Z7∗是循环群,群元素有1.2.3.4.5.6,其中只有3和5可以生成此群,能找到生成元。
⟨1⟩生成(1)⟨2⟩生成(2,4,6)⟨3⟩生成(3,2,6,4,5,1)⟨4⟩生成(4,2,1)⟨5⟩生成(5,4,6,2,3,1)⟨6⟩生成(6,1)\langle1\rangle生成(1)\\
\langle2\rangle生成(2,4,6)\\
\langle3\rangle生成(3,2,6,4,5,1)\\
\langle4\rangle生成(4,2,1)\ ...
对称和分组密码的审计
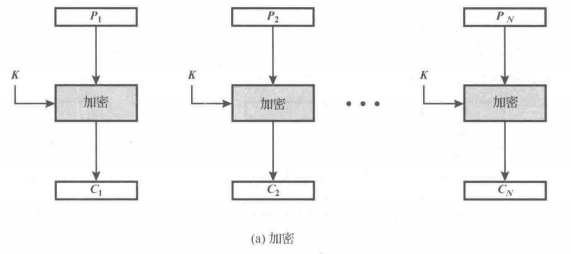
一、分组密码模式
ECB(电子密码本)
每个分组独立加密,互不干扰,分组大小根据加密算法确定,如DES需要64bits,也就是8字节
Geek Challenge 2023的Simple3DES,当明文恰好8字节的整数倍,padding时会再填充一个确定字节串,出先漏洞。
引自Geek Challenge 2023 | Lazzaro (lazzzaro.github.io)
区块链
一、关键字
价值转移 第三方 去第三方 比特币 SET 盲签 双花 工作量证明 区块链 去中心化 比特币钱包 挖矿 以太坊 智能合约 EOS 公有链 交易回滚 哈希指针 梅克尔树 分布式数据库 激励机制 分布式共识 拜占庭将军问题
ElGamal的CCA攻击
ElGamal的CCA攻击
Alice:
Bob:
Alice:
假设有一个解密机,Bob将本来要发给Alice的密文(c1,c2)输入到解密机,即可以获得明文m
如果有一组密文C*(c1,c2)无法输入到解密机,如何得到它的明文m*
正常来讲,传入解密机的数据时[gr,(gx)r∗m][g^r,(g^x)^r*m][gr,(gx)r∗m],解密机和Alice一样,拥有私钥x,它可以得到[(gr)x,(gx)r∗m][(g^r)^x,(g^x)^r*m][(gr)x,(gx)r∗m],第二项除以第一项即可得到m
但是我们不能传入密文C*,于是构造传入数据[grgr′,(gx)r∗m∗(gx)r′]=[gr+r′,(gx)r+r′∗m][g^rg^{r'},(g^x)^r *m*(g^x)^{r'}]=[g^{r+r'},(g^x)^{r+r'}*m][grgr′,(gx)r∗m∗(gx)r′]=[gr+r′,(gx)r+r′∗m],解密机凭借私钥得到[(gr+r′)x,(gx)r+r′∗m][(g^{r+r'})^x,(g^x)^{r+r'}*m][(gr+r′)x,(gx)r+r′∗ ...
连分数攻击
密码学学习笔记之连分数 | Van1sh的小屋 (jayxv.github.io)
勒让德定理,满足定理可用连分数近似
c = N1 = N2 = e = cf = continued_fraction(Integer(N1) / Integer(N2))i = 1while 1: q1 = cf.numerator(i) q2 = cf.denominator(i) if N1 % q1 == 0 and q1 != 1: print(q1) p1 = N1 // q1 d = gmpy2.invert(e,(p1-1)*(q1-1)) m = pow(c,d,N1) flag = long_to_bytes(int(m)) if b"ISCTF" in flag: print(flag) break i += 1
ComSec2
简答题(回答可以是中文也可以是英文):
1、What is the difference between diffusion and confusion?
扩散是将明文的冗余度分散到密文中,明文中的一位会影响密文中的许多位,产生扩散的最简单方法是“置换”。
混淆是使用秘钥与密文之间关系复杂化,通常使用非线性代换让统计关系极小化。
所以,扩散是作用于明文和密文的关系,混淆是作用于秘钥和密文的关系。
2、What was the original set of criteria used by NIST to evaluate candidate AES ciphers?
安全性、成本、算法和实现特征
编程题:
1、使用C或者Python语言,写一个函数完成GF(2^8)中任意两个元素的乘法。
本题的操作对象是把多项式系数看成二进制比特串,以字符串的形式存储起来。
主体函数是一个异或函数xoradd和一个乘法函数mul。
GF(2^8)中的元素都是8位。
乘法mul()函数是用简单算法实现的,省去了要模既约多项式要用到的除法。
实现:
def xoradd(P1,P2): res=' ...
离散对数问题
一、调用函数
x=logxbx=\log_xbx=logxb写成函数为discrete_log(x,b,order,operation)
二、Pohlig-Hellman算法
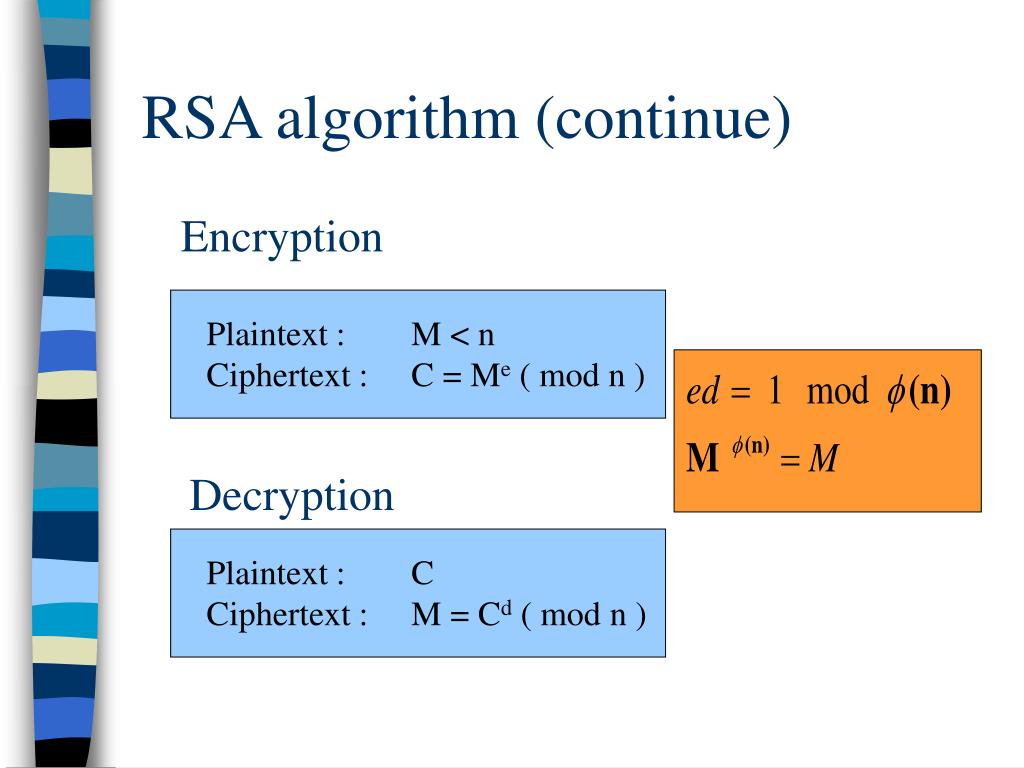
多项式RSA
原理
多项式RSA适用于整数RSA原理。
多项式所在的域叫做有限域。整数域上的素数p和q,在有限域上有与之对应的是不可约多项式g§和g(q),即不能进行因式分解的多项式。
g(n)=g§*g(q),再计算g(n)的欧拉函数φ,选取整数e作为公钥,e须与φ互素,才能保证有乘法逆元d,也就是私钥。
加密过程
g(m)e≡g(c) mod g(n)g(m)^{e}\equiv g(c) \bmod g(n)
g(m)e≡g(c)modg(n)
解密过程就是反过来,根据φ求出d即可解出,易证。
对于不可约多项式的φ,如何求?首先,欧拉函数是小于n的所有与n互素的数的个数。也就是这个多项式环的阶,即环中所有元素个数,对于一个系数模p,最高次为n-1的多项式来说,元素个数为p^n-1。
脚本
#sage1#已知p=2,n,e,cp=P=PolynomialRing(Zmod(p),name='x')#建立多项式环x=P.gen()#x为环的生成多项式e=n=c=#分解nq1,q2=n.factor()q1,q2=q1[0],q2[0]#求φphi=(p^q1.degree()-1)*(p^q2.d ...
pwntool实现C/S交互
socketserver交互
class Task(socketserver.BaseRequestHandler): def __init__(self, *args, **kargs): super().__init__(*args, **kargs) #super用来调用父类的构造函数,并将相应的参数传递给父类
工作认证
def proof_of_work(self): random.seed(urandom(9)) proof = ''.join([random.choice(string.ascii_letters + string.digits) for _ in range(16)]) digest = sha256(proof.encode()).hexdigest() self.dosend('sha256(XXXX + {}) == {}'.format(proof[4:], digest) + "\n" + '@ XXXX=') x = self.request.recv(10) x = (x. ...
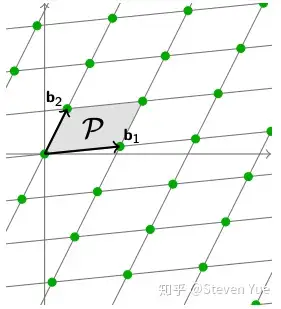
Lattices
∥v∥≤ndet(L)1/n\|v\|\leq \sqrt n \det (L) ^ {1/n}
∥v∥≤ndet(L)1/n
一个n×n的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:
A=matrix([[1,h],[0,p]])lll=A.LLL()F,G=lll[0]F,G=abs(F),abs(G)