简答题（回答可以是中文也可以是英文）：

1、What is the difference between diffusion and confusion?

扩散是将明文的冗余度分散到密文中，明文中的一位会影响密文中的许多位，产生扩散的最简单方法是“置换”。

混淆是使用秘钥与密文之间关系复杂化，通常使用非线性代换让统计关系极小化。

所以，扩散是作用于明文和密文的关系，混淆是作用于秘钥和密文的关系。

2、What was the original set of criteria used by NIST to evaluate candidate AES ciphers?

安全性、成本、算法和实现特征

编程题：

1、使用C或者Python语言，写一个函数完成GF(2^8)中任意两个元素的乘法。

本题的操作对象是把多项式系数看成二进制比特串，以字符串的形式存储起来。
主体函数是一个异或函数xoradd和一个乘法函数mul。
GF(2^8)中的元素都是8位。
乘法mul()函数是用简单算法实现的，省去了要模既约多项式要用到的除法。
实现：

def xoradd(P1,P2):
    res=''
    for i in range(8):
        res+=str(int(P1[i]) ^ int(P2[i]))
    return res

def mul(P1,P2):
    res='00000000'
    # 设置为AES使用的既约多项式
    ReducedPoly = '100011011'
    for i in range(8):
        if P2[7-i]=='1':
            res=xoradd(res,P1)
        if P1[0]=='1':
            P1=xoradd(P1[1::]+'0',ReducedPoly[1::])
        else:
            P1=P1[1::]+'0'
    return res

def toPoly(P):
    poly=['x^7','x^6','x^5','x^4','x^3','x^2','x','1']
    res=''
    for i in range(len(P)):
        if P[i]=='1':
            res=res+poly[i]+'+'
    if res[-1]=='+':
        res=res[0:-1]
    return res;

def main():
    print('请输入多项式系数：')
    a=input()
    b=input()
    c=mul(a,b)
    print(toPoly(a)+'  与  '+toPoly(b)+'  的乘积为  '+toPoly(c))

if __name__=='__main__':
    main()

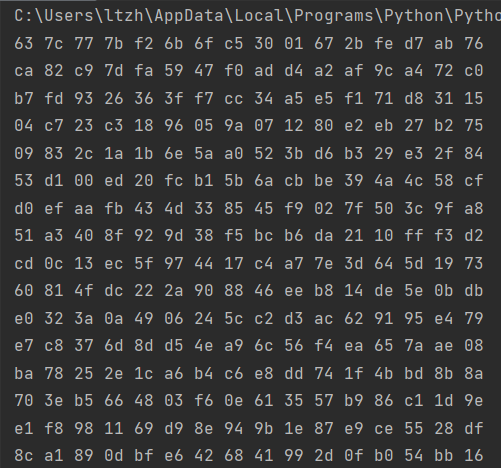
运行结果：

image-20231023173017229

2、使用C或者Python语言，写一个程序生成AES算法中使用的S-Box。

要实现S-Box，分三步
（1）产生一个初始化S盒
（2）元素求逆在GF(2^8)中
（3）字节移位
求逆算法使用多项式的egcd，需要实现乘法、除法、异或加。实现除法要先实现乘法，因为上个实验用的是简便算法实现乘法，适用于8位，而本实验的除法涉及到9位，所以要重新写一般形式的乘法。
实现：

def genBox():
    n=16
    #box值用字符串存储
    box=[[str(hex(row)[2:])+str(hex(col)[2:]) for col in range(n)] for row in range(n)]
    return box

def xoradd(P1,P2):
    res=''
    #P1和P2长度相等
    P1=P1.zfill(len(P2))
    P2=P2.zfill(len(P1))

    for i in range(len(P1)):
        res+=str((int(P1[i])) ^ int(P2[i]))
    return res

def hex2bits(str):
    bits=bin(int(str,16))[2:].zfill(8)
    return bits

def bits2hex(bits):
    str=hex(int(bits[0:4],2))[2:]+hex(int(bits[4::],2))[2:]
    return str

def div(Abit,Bbit):#A为被除数，B为除数
    Qbit=''
    while True:
        #消去字符串前导0
        Abit=Abit.lstrip('0')
        Bbit=Bbit.lstrip('0')
        if Abit=='':Abit+='0'
        if Bbit=='':Bbit+='0'

        if int(Abit,2)<int(Bbit,2):#如果被除数小于除数，即除尽
            Q=list('000000000')
            for i in range(len(Qbit)):
                Q[8-int(Qbit[i])]='1'
            Q=''.join(Q)
            return (Q,Abit)
        else:
            q=len(Abit)-len(Bbit)
            Qbit+=str(q)#存储商多项式各项的指数
            temp=Bbit+q*'0'
            r=xoradd(Abit,temp)#余数
            Abit=r#余数作为被除数

def mul(P1,P2):
    # 设置为AES使用的既约多项式
    res='0'
    ReducedPoly = '100011011'
    for i in range(len(P2)):
        if P2[i]=='1':
            temp=P1+(len(P2)-i-1)*'0'
            res=xoradd(res,temp)
    return div(res,ReducedPoly)[1]

def Poly_egcd(a,b):#a为素多项式
    #0的逆元还是0
    if b=='00000000': return '00000000'

    r0,r1,s0,s1='1','0','0','1'
    while(b.count('1')!=False):#如果b为0
        q,a,b=div(a,b)[0],b,div(a,b)[1]
        r0,r1=r1,xoradd(r0,mul(q,r1))
        s0,s1=s1,xoradd(s0,mul(q,s1))
    return s0

def mov(bits):
    cbit=str(bin(int('63',16)))[2:].zfill(8) #c为63
    bits=bits.zfill(8)
    newbits=list()
    #移位操作
    for i in range(len(bits)):
        newbits.append(str(int(bits[i])^int(bits[(i+4)%8])^int(bits[(i+3)%8])^int(bits[(i+2)%8])^int(bits[(i+1)%8])^int(cbit[i])))
    newbits=''.join(newbits)
    return newbits

def S_BOX():
    box=genBox()
    # 设置为AES使用的既约多项式
    ReducedPoly = '100011011'

    for i in range(len(box)):
        for j in range(len(box[i])):
            h=hex2bits(box[i][j])             #十六进制转二进制
            temp=mov(Poly_egcd(ReducedPoly,h))#求逆+移位
            box[i][j]=bits2hex(temp)          #二进制转十六进制
            print(box[i][j],end=' ')
        print()
    return  box

def main():
    box=S_BOX()

if __name__ =='__main__':
    main()

运行结果：

image-20231023174545331