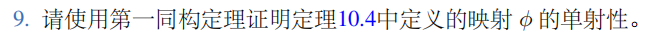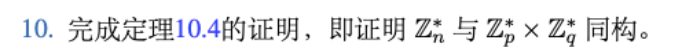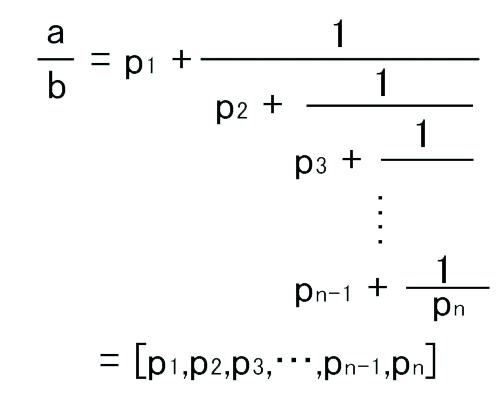image-20221125141329673

image-20240119215050777

image-20221125144102349

1.令M=∏i=14mi=3465根据egcda1=1,b1=M/m1=693,b1−1=2 mod 5a2=2,b2=M/m2=495,b2−1=3 mod 7a3=3,b3=M/m3=385,b3−1=4 mod 9a4=4,b4=M/m4=315,b4−1=8 mod 11x=∑i=1n=aibibi−1=19056≡1731 mod M∴x=17311.令M=\prod_{i=1}^4m_i=3465\\ 根据egcd\\ a_1=1,b_1=M/m_1=693,b_1^{-1}=2\bmod 5\\ a_2=2,b_2=M/m_2=495,b_2^{-1}=3\bmod 7\\ a_3=3,b_3=M/m_3=385,b_3^{-1}=4\bmod 9\\ a_4=4,b_4=M/m_4=315,b_4^{-1}=8\bmod 11\\ x=\sum_{i=1}^{n}=a_ib_ib_i^{-1}=19056\equiv1731\bmod M\\ \therefore x=1731

image-20221125151940362

221=n=17∗13∴2000↔(11,11)20002019 mod 221=(112019 mod 17,112019 mod 13)根据费马小定理=(11126∗16+3 mod 17,11168∗12+3 mod 13)=(113 mod 17,113 mod 13)=(5,5)∴x≡5 mod 17x≡5 mod 13根据CRT或解方程易得x=5∴20002019( mod 221)=5221=n=17*13\\ \therefore 2000\leftrightarrow(11,11)\\ 2000^{2019}\bmod 221=(11^{2019}\bmod 17,11^{2019}\bmod 13)\\根据费马小定理\\ =(11^{126*16+3}\bmod 17,11^{168*12+3}\bmod 13)\\=(11^3\bmod 17,11^3\bmod 13)=(5,5)\\ \therefore x\equiv5\bmod 17\\ x\equiv5\bmod 13\\ 根据CRT或解方程易得x=5\\ \therefore 2000^{2019} (\bmod221)=5

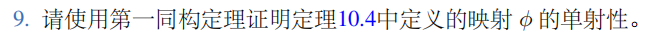
image-20221125164740346

image-20221125171131154

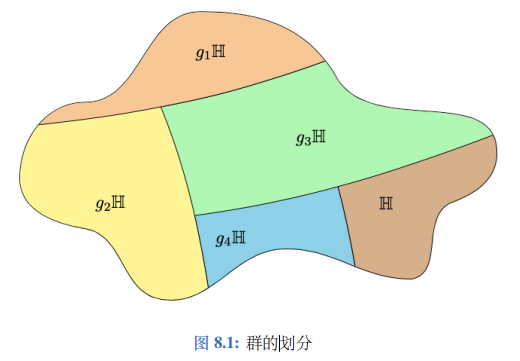
(1)定义从Zn到Zp×Zq的映射ϕ:ϕ(x)=([x mod p],[x mod q])易得ϕ(x)上的单位元e是(0,0),对∀x∈Zn,有ϕ(x)=([x mod p],[x mod q])=(0,0)当且仅当x=0,∴K=Kerϕ={0},∵x=0又是Zn的单位元，∴K是正规子群∴∃唯一同构映射η:Zn/K→ϕ(Zn)设ψ:Zn→Zn/K是标准同态∵K的阶是1∴Zn/K和Zn有相同的阶即对于∀gK∈Zn/K,都有g∈Zn∴ψ是单射∵ϕ=ηψ∴ϕ是单射(2)定义从Zn∗到Zp∗×Zq∗的映射ϕ,同理此时ϕ(x)上的单位元为(1,1)对∀x∈Zn,有ϕ(x)=([x mod p],[x mod q])=(1,1)当且仅当x=1,∴此时K=1,下面的证明与(1)同理，只有Kerϕ不一样。(1)定义从Z_n到Z_p\times Z_q的映射\phi:\\ \phi(x)=( [x\bmod p],[x\bmod q] )\\ 易得\phi(x)上的单位元e是(0,0),\\ 对\forall x \in Z_n,有\phi(x)=( [x\bmod p],[x\bmod q] )=(0,0)\\ 当且仅当x=0,\\ \therefore K=Ker\phi=\{0\},\\ \because x=0 又是Z_n的单位元，\\ \therefore K是正规子群\\ \therefore \exist唯一同构映射\eta:Z_n/K\rightarrow \phi(Z_n)\\ 设\psi:Z_n\rightarrow Z_n/K是标准同态\\ \because K的阶是1\\ \therefore Z_n/K和Z_n有相同的阶\\ 即对于\forall gK\in Z_n/K,都有g\in Z_n\\ \therefore \psi是单射\\ \because \phi=\eta\psi\\ \therefore \phi是单射\\ (2)定义从Z_n^*到Z_p^*\times Z_q^*的映射\phi,\\ 同理此时\phi(x)上的单位元为(1,1)\\ 对\forall x\in Z_n,有\phi(x)=( [x\bmod p],[x\bmod q] )=(1,1)\\ 当且仅当x=1,\\ \therefore 此时K={1},\\ 下面的证明与(1)同理，只有Ker\phi不一样。

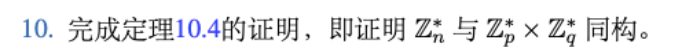
image-20221125233610715

1.定义从Zn∗到Zp∗×Zq∗的映射ϕ为:ϕ(x)=([x mod p],[x mod q])2.根据中国剩余定理，任意序对中的两个同余式在模n下有唯一解所以满射显然3.根据中国剩余定理，∀a,b<n,有([a mod p],[a mod q])=([b mod p],[b mod q]),∵解唯一,则a=b,满足单射。4.∵ϕ(a×b)=([(a×b) mod p],[(a×b) mod q])=([a mod p],[a mod q])×([b mod p],[b mod q])=ϕ(a)×ϕ(b)∴ϕ满足群操作∴Zn∗和Zp∗×Zq∗同构1.定义从Z_n^*到Z_p^*\times Z_q^*的映射\phi为:\\ \phi(x)=( [x\bmod p],[x\bmod q] )\\ 2.根据中国剩余定理，任意序对中的两个同余式在模n下有唯一解\\ 所以满射显然\\ 3.根据中国剩余定理，\forall a,b<n,\\ 有( [a\bmod p],[a\bmod q] )=( [b\bmod p],[b\bmod q] ),\\ \because解唯一,则a=b,满足单射。\\ 4.\because \phi(a\times b)=( [(a\times b)\bmod p],[ (a\times b)\bmod q] )\\ =( [a\bmod p],[a\bmod q] )\times( [b\bmod p],[b\bmod q] )\\ =\phi(a)\times\phi(b)\\ \therefore \phi 满足群操作 \therefore Z_n^*和Z_p^*\times Z_q^*同构