CINTA第九章

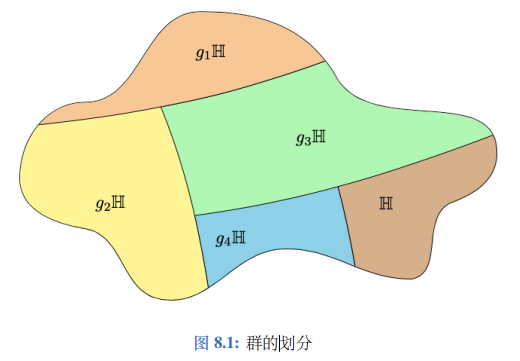
4. 根据命题9.5，H是G的正规子群当且仅当对任意g∈G，有 gHg −1 = H。实 际上，条件可以放松到只证明 gHg −1 ⊂ H。请给出证明。

$$\because\forall g\in G,gHg^{-1}\subset H,\\ \therefore gH\subset Hg,\\ \therefore H\subset g^{-1}Hg\\ \therefore H\subset g^{-1}H(g^{-1})^{-1}\\ 即H\subset gHg^{-1}\\ \because gHg^{-1}\subset H\\ \therefore gHg^{-1}=H\\ \therefore gH=Hg\\ \therefore H是G的正规子群.$$

5. 定义映射 ϕ : G → G 为：g → g 2。请证明 ϕ 是一种群同态当且仅当 G 是阿贝尔群。

   $$\Rightarrow:\\ \because \phi是一种群同态,\\ \therefore\forall a,b\in G,\phi(a\cdot b)=\phi(a)\circ\phi(b)=a^2\circ b^2,\\ \because \phi:G\rightarrow H:g\rightarrow g^2,\\ \therefore\phi(a\cdot b)=(a\cdot b)^2=b^2\circ a^2,\\ \because a^2\circ b^2=b^2\circ a^2,\\ \therefore G是阿贝尔群\\ \Leftarrow:\\ \because G是阿贝尔群\\ \therefore \forall a,b\in G,\phi(a\cdot b)=(a\cdot b)^2=b^2a^2\\ =a^2b^2=\phi(a)\circ\phi(b)\\ \therefore \phi是一种群同态$$

6. 设 ϕ : G → H 是一种群同态。请证明：如果 G 是循环群，则 ϕ(G) 也是循环群；如果 G 是交换群，则 ϕ(G) 也是交换群。

$$(1)\\ \because G是循环群，\\ \therefore \exist g是G的生成元，\\ 且\forall c\in G,都有a,b\in G,a\cdot b=c\\ \because \phi:G\rightarrow H是群同态\\ \therefore \phi(a\cdot b)=\phi(a)\circ\phi(b)=\phi(c)\\ 即\phi(g\cdot g)=\phi(g)\circ\phi(g)=\phi(g^2)=\phi(g)^2\\ 同理有\phi(g^n)=\phi(g)^n\\ 即\phi(G)中的元素都可由由\phi(G)中的生成元\phi(g)形成\\ \therefore\phi(G)也是循环群。\\ (2)\\ \because G是交换群\\ \therefore\forall a,b\in G,有a\cdot b=b\cdot a\\ \because \phi:G\rightarrow H是群同态\\ \therefore\phi(a\cdot b)=\phi(a)\circ\phi(b)\\ \phi(b\cdot a)=\phi(b)\circ\phi(a)\\ \therefore\phi(a)\circ\phi(b)=\phi(b)\circ\phi(a)\\ \therefore \phi(G)是阿贝尔群$$

7. 证明：如果 H 是群 G 上指标为 2 的子群，则 H 是 G 的正规子群。

   $$(1)若a\notin H,则aH\neq H,Ha\neq H,\\ \because H是群G上指标为2的子群,\\ 且易知左陪集和右陪集元素个数相等\\ \therefore G=H\cup Ha=H\cup aH,\\ \therefore aH=Ha\\ (2)若a\in H,则aH=Ha=H\\ 综上，H是G的正规子群$$