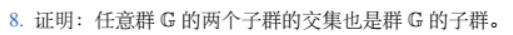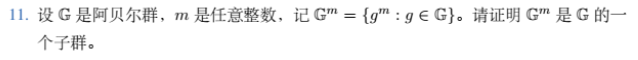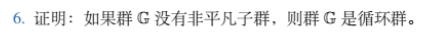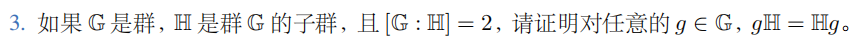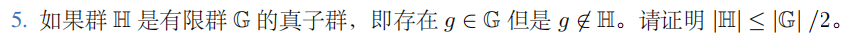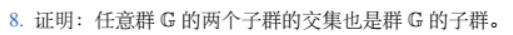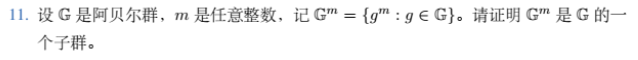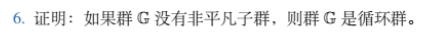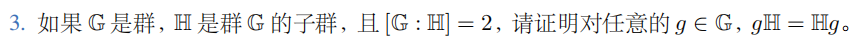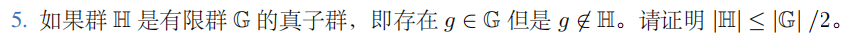第六章 群与子群

image-20221027211517226

因为根据结合律g0g1...gn∗gn−1...g1−1g0−1=g0g1...e...g1−1g0−1=e又因为gn−1...g1−1g0−1∗g0g1...gn=g1−1g0−1...e...g0g1...e=e所以g0g1...gn的逆元是gn−1...g1−1g0−1。因为根据结合律g_0g_1...g_n*g_n^{-1}...g_1^{-1}g_0^{-1}\\ =g_0g_1...e...g_1^{-1}g_0^{-1}=e\\ 又因为g_n^{-1}...g_1^{-1}g_0^{-1}*g_0g_1...g_n\\ =g_1^{-1}g_0^{-1}...e...g_0g_1...e=e\\ 所以g_0g_1...g_n的逆元是g_n^{-1}...g_1^{-1}g_0^{-1}。

image-20221027213259937

(1)G的两个子群的交集必是G的子集，这是显然的。(2)假设G的两个子群为H1,H2,其交集为I封闭性：对于∀a,b∈I,因为I是G1和G2的子集，所以a，b也在G1和G2里，又因为G1和G2是群所以存在ab∈G1∩G2即∃ab∈I,满足封闭性。结合律：这是显然的，加法、乘法都满足结合律单位元：因为∃a∈I,则a也在G1和G2里，因为G1和G2是群，所以存在e在G1和G2中，因为单位元唯一性，e在G1和G2的交集中即∃e∈I,使得ea=ae=a.逆元：与单位元同理，是存在逆元的。所以，I是群综上，任意群G的两个子群的交集也是群G的子群。(1)G的两个子群的交集必是G的子集，这是显然的。\\ (2)假设G的两个子群为H_1,H_2,其交集为I\\ 封闭性：\\ 对于\forall a,b \in I,因为I是G_1和G_2的子集，\\ 所以a，b也在G_1和G_2里，又因为G_1和G_2是群\\ 所以存在ab\in G_1\cap G_2\\ 即\exists ab \in I,满足封闭性。\\ 结合律：\\ 这是显然的，加法、乘法都满足结合律\\ 单位元：\\ 因为\exist a\in I,则a也在G_1和G_2里，\\ 因为G_1和G_2是群，所以存在e在G_1和G_2中，\\ 因为单位元唯一性，e在G_1和G_2的交集中\\ 即\exist e\in I,使得ea=ae=a.\\ 逆元：\\ 与单位元同理，是存在逆元的。\\ 所以，I是群\\ 综上，任意群G的两个子群的交集也是群G的子群。\\

image-20221028000906079

(1)因为H和K是G的子群，所以对于∀hk∈HK,即h∈H,k∈K,都有h、k∈G,即hk∈G,所以HK是G的子集。(2)封闭性： 假设a∈H,b∈H,因为H是子群，所以ab∈H,假设c∈K,d∈K,因为K是子群，所以cd∈K,根据定义，所以abcd∈HK,且ac∈HK,bd∈HK,则对于∀ac∈HK,bd∈HK,又因为是阿贝尔群，都有acbd=abcd∈HK,封闭性得证。逆元：假设a∈H,因为H是子群，所以a−1∈H,假设b∈K,因为K是子群，所以b−1∈K,根据定义，ab∈HK,a−1b−1∈HK,因为是阿贝尔群，所以∀ab∈HK,都有(ab)−1=a−1b−1∈HK.综上，因为HK是子集，证出封闭性和逆元即可得出是子群的结论。如果不是阿贝尔群，不满足交换律，∴结论不成立。(1)因为H和K是G的子群，\\ 所以对于\forall hk\in HK,即h\in H,k\in K,\\ 都有h、k\in G,即hk\in G,\\ 所以HK是G的子集。\\ (2)封闭性：\\\ 假设a\in H,b\in H,因为H是子群，所以ab\in H,\\ 假设c\in K,d\in K,因为K是子群，所以cd\in K,\\ 根据定义，所以abcd\in HK,\\ 且ac\in HK,bd\in HK,\\ 则对于\forall ac\in HK,bd\in HK,\\ 又因为是阿贝尔群，都有acbd=abcd\in HK,\\ 封闭性得证。\\ 逆元：\\ 假设a\in H,因为H是子群，所以a^{-1}\in H,\\ 假设b\in K,因为K是子群，所以b^{-1}\in K,\\ 根据定义，ab\in HK,a^{-1}b^{-1}\in HK,\\ 因为是阿贝尔群，所以\forall ab\in HK,\\ 都有(ab)^{-1}=a^{-1}b^{-1}\in HK.\\ 综上，因为HK是子集，证出封闭性和逆元即可得出是子群的结论。\\ \\ 如果不是阿贝尔群，不满足交换律，\\ \therefore 结论不成立。

image-20221029202512415

(1)根据费马小定理，gm∈G,即Gm是G的子集。(2)假设∀g1m,g2m∈Gm，因为g2∈G,则g2−1∈G,根据定义(g2−1)m∈Gm,又因为g1g2−1∈G,所以(g1g2−1)m∈Gm,因为G是阿贝尔群，所以(g1g2−1)m=g1m(g2m)−1∈Gm.根据命题群G非空子集H是G子群，当且仅当对任意a,b∈H,ab−1∈H得证。(1)根据费马小定理，g^m\in G,即G^m是G的子集。\\ (2)假设\forall g_1^m,g_2^m\in G^m，\\ 因为g_2\in G,则g_2^{-1}\in G,\\ 根据定义(g_2^{-1})^m\in G^m,\\ 又因为g_1g_2^{-1}\in G,所以(g_1g_2^{-1})^m\in G^m,\\ 因为G是阿贝尔群，所以(g_1g_2^{-1})^{m}=g_1^m(g_2^m)^{-1}\in G^m.\\ 根据命题群G非空子集H是G子群，当且仅当对任意a,b∈H,ab^{-1}∈H得证。

image-20221104150420305

即证，G的子群群只有非平凡子群{e}，则群G是循环群。则G中任意非e的元素都能生成G即∀g∈G,集合<g>={gk:k∈Z}=G，则称G是为g生成的循环群即证，G的子群群只有非平凡子群\{e\}，则群G是循环群。\\ 则G中任意非e的元素都能生成G\\ 即\forall g\in G,集合<g>=\{g^k:k\in Z\}=G，\\ 则称G是为g生成的循环群

image-20221030193142089

设G的阶为q，对于∀g∈G,gn=e,根据除法算法，∃q,r∈Z使得n=qk+r(0≤r<k)设k为g的阶，∀g∈G,gk=e,因此，e=gn=gkq+r=gkqgr=gr.解得r=0,所以n=kq,得证循环群G中任意元素的阶都整除群G的阶。设G的阶为q，\\ 对于\forall g\in G,g^n=e,\\ 根据除法算法，\exists q,r\in Z使得n=qk+r(0\leq r<k)\\ 设k为g的阶，\forall g\in G,g^k=e,\\ 因此，e=g^n=g^{kq+r}=g^{kq}g^r=g^r.\\ 解得r=0,所以n=kq,\\ 得证循环群G中任意元素的阶都整除群G的阶。\\

image-20221030210152001

import math
from cmath import sqrt
from math import ceil

def prime(n):#判定素数
    for i in range(2,int(math.sqrt(n))+1):
        if n % i == 0:
            return False
    return True

def prime_factors_list(n):#获取素数列表
    ls=[]
    for i in range(2,n):
        if prime(i):
            ls.append(i)
    return ls

def is_primitive_root(a,p):#判定生成元
    flist=prime_factors_list(p-1)
    for f in flist:
        if pow(a,(p-1)//f,p)==1:
            return False
        return True

def get_minroot(p):#获取最小生成元
    if not prime(p):
        return False
    elif p==2:
        return 1
    for i in range(2,p-1):
        if is_primitive_root(i,p):
            return i
    return False

def P_of_maxroot(n):#最大生成元的素数P
    ls=prime_factors_list(n)
    root=[]
    for i in ls:
        root.append(get_minroot(i))
    d=dict(zip(ls,root))
    print(d)
    return max(d,key=lambda k:d[k])

调用P_of_maxroot函数即可，最大的最小生成元是11

第八章 陪集与拉格朗日定理

image-20221101125732030

(1)若g∉H,则gH≠H,Hg≠H,∵G有两个左陪集，∴G=H∪Hg=H∪gH∴gH=Hg=G−H(2)若g∈H,则gH=Hg=H综上，gH=Hg.(1)若g\notin H,则gH\neq H,Hg\neq H,\\ \because G有两个左陪集，\\ \therefore G=H\cup Hg=H\cup gH\\ \therefore gH=Hg=G-H\\ (2)若g\in H,则gH=Hg=H\\ 综上，gH=Hg.

image-20221104155302248

根据拉格朗日定理，子群的阶整除群的阶所以子群H的阶为p、q、1，H的阶为1时，{e}是循环群，因为p、q是素数，素数阶的群一定是循环群.所以G的任意真子群是循环群。根据拉格朗日定理，子群的阶整除群的阶\\ 所以子群H的阶为p、q、1，\\ H的阶为1时，\{e\}是循环群，\\ 因为p、q是素数，素数阶的群一定是循环群.\\ 所以G的任意真子群是循环群。

image-20221104155316079

∵群H是有限群G的真子群，根据拉格朗日定理∴G上被划分的左陪集≥2,即∣G∣/∣H∣≥2∴∣H∣≤∣G∣/2\because 群H是有限群G的真子群，根据拉格朗日定理\\ \therefore G上被划分的左陪集\geq 2,即|G|/|H|\geq 2\\ \therefore |H|\leq|G|/2